预测市场的“陷阱”：为什么你买的总是输
作者：Terry Lee
原标题：Why prediction markets are mispricing parlays – the correlation blind spot
编译及整理：BitpushNews
前言
在像 Polymarket 这样的平台上，大多数人（包括曾经的我）对“串关”（Parlay，即多重事件组合投注）的定价方式通常是：将每一项事件的概率简单相乘。
例如：
-
事件 A 发生的概率 P(A) = 80%
-
事件 B 发生的概率 P(B) = 70%
-
事件 C 发生的概率 P(C) = 60%
那么，串关总概率 = 80% × 70% × 60% = 33.6%
（注意，Parlays 是博彩和投资中的术语，中文通常叫“串关”或“过关”。定义： 你把两个或多个独立的事件赌注绑在一起。规则： 只有当你选的所有事件全部预测正确，你才能拿奖金。只要其中一个错了，整个注单就全赔。）
听起来很简单，对吧？
问题不在于数学计算，而在于隐藏的假设。
这种乘法运算的前提是假设每个事件都是相互独立的。这意味着 A 的结果对 B 没有任何影响。但在现实中，情况并非如此。
例如：
-
美联储在某次会议上的决定会严重影响下一次会议。
-
一位总统候选人赢得了“铁锈地带”各州，预示着他在宾夕法尼亚州的胜算，进而影响整个总统大选的胜率。
现实中，绝大多数值得做“串关”的事件都是有关联的。如果你忽略了这种关联性，你极有可能支付了过高的价格，或者错失了赚钱的机会。
本文将展示一个简单的框架，教你如何像传统金融行业几十年来为“多腿期权”（Multi-leg options）定价那样，为串关进行科学定价。
为什么会存在定价错误？
在我看来，大多数预测市场工具都侧重于“执行”，而非“相关性分析”。此外，这类细分市场相对尚不成熟。虽然“串关”在体育博彩中很常见，但在处理特定社会/经济事件时，由于市场还处于早期阶段，定价机制尚未完善。
案例研究：美联储利率决议
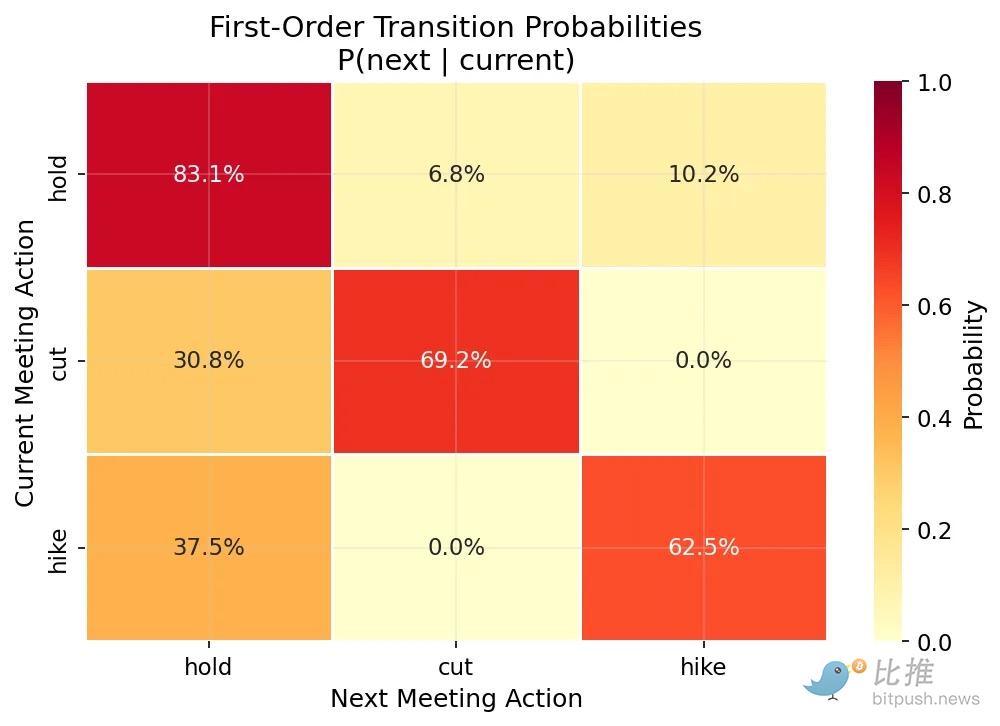
（图1：美联储倾向于重复动作，83% 的情况下“维持利率”后会再次“维持”）
利用圣路易斯联储（FRED）的数据（从 1994 年到 2026 年初），我构建了一个转移矩阵（Transition Matrix），专门提取美联储在连续两次会议之间的决策变化。
结果非常明确：
显然，美联储的运作具有“连贯性”。作为一个前瞻性、依赖数据的机构，他们倾向于重复同样的动作，直到发生“制度性转变”（Regime Shift）。
这种“连贯性”有多强？
为了测试这一点，我建立了一个模型来识别历史上每一次连续的“决策趋势”（即每一次连续的维持、降息或加息周期）。
结果如下：
-
维持利率： 共出现 32 次趋势，平均每次持续 5.4 个会议。
-
降息： 共出现 12 次趋势，平均每次持续 3.3 个会议。
接着，我模拟了 1000 个“平行宇宙”中的美联储历史。在这些模拟中，每次会议都是独立的（类似抛硬币）。基于历史总数据，设定维持概率为 66%，降息为 15%，加息为 19%，但每次决策之间没有任何关联。
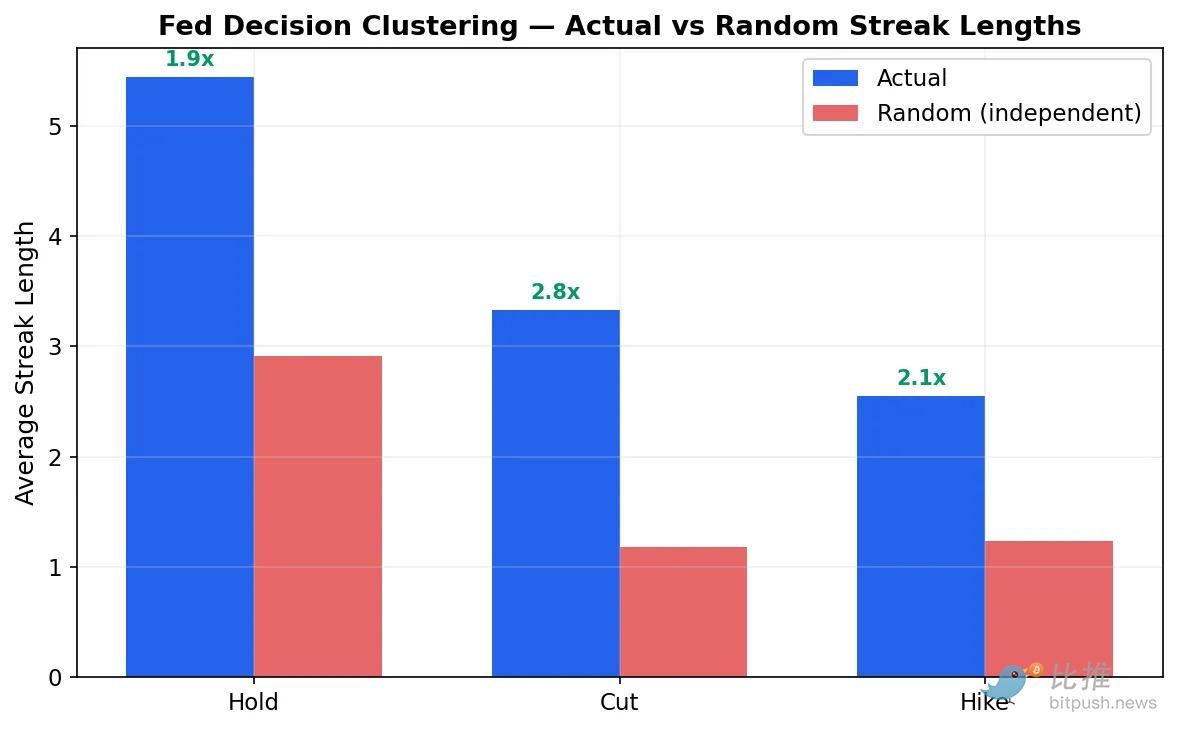
（图2：美联储的实际决策连贯性是随机概率的 2-3 倍）
在“相互独立”的模拟假设下，维持利率的趋势平均仅能持续 2.9 个会议，而降息和加息则平均只有 1.2 个会议。
将实际历史与随机模拟进行对比：
-
维持： 实际 5.4 次 vs 随机 2.9 次（长了 1.9 倍）
-
降息： 实际 3.3 次 vs 随机 1.2 次（长了 2.8 倍）
-
加息： 实际 2.6 次 vs 随机 1.2 次（长了 2.1 倍）
值得注意的是，降息的连贯性几乎是随机概率的三倍。 原因是：当美联储开始降息时，通常是为了应对持续的经济恶化，这种问题不可能在一次会议内解决。他们降息，评估数据，如果数据依然糟糕，他们极大概率会再次降息。
简单乘法计算“串关”完全忽略了这些相关性。现实产生的连贯性比独立随机模型强 2-3 倍。
连续两次会议后会发生什么？
仅仅看上一次会议是不够的，定价“三关”（三个事件组合）需要研究基于前两次会议结果的条件概率。
分析可以分为两个部分：
延续原有路径
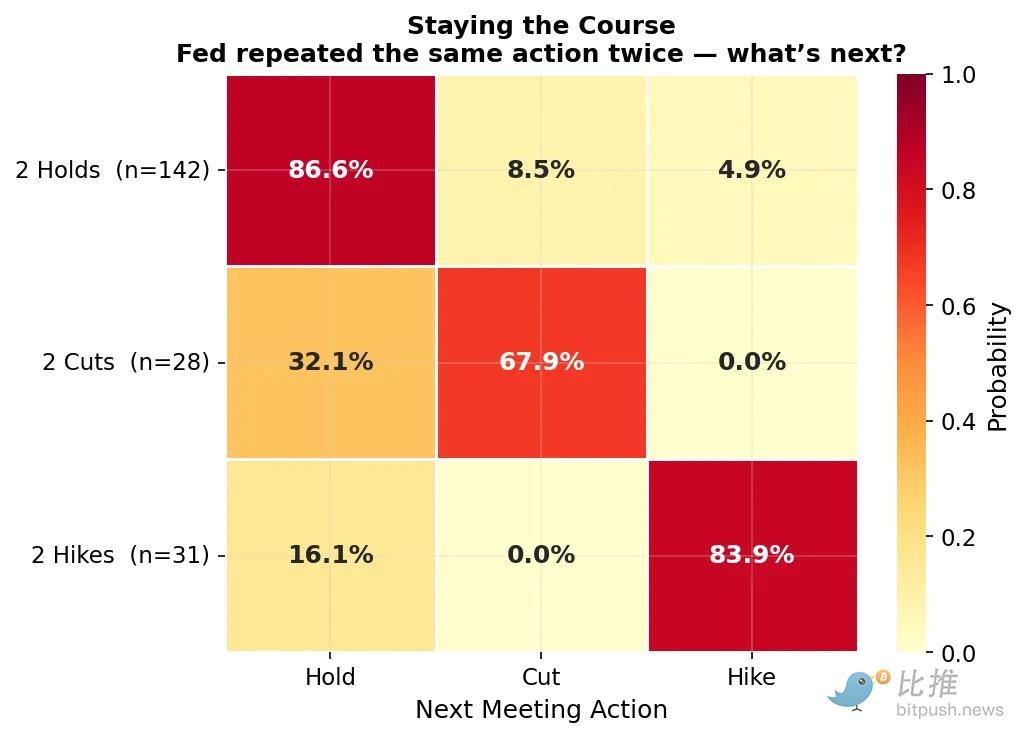
（图3：在两次相同操作后，第三次操作几乎总是匹配的）
从图 3 可以清楚地看到，当美联储重复同样的动作两次后，第三次继续该动作的概率是压倒性的：
-
两次维持 -> 第三次维持： 87%
-
两次加息 -> 第三次加息： 84%
-
两次降息 -> 第三次降息： 68%（略弱一些）
同样值得注意的是矩阵中 0% 的单元格：美联储从未在连续两次加息后突然降息，也从未在连续两次降息后突然加息。他们总是先经过一个“暂停（维持）”阶段。仅仅意识到这一点，就能帮你排除掉一系列“幼稚模型”认为有价值的无效组合。
制度转变之后
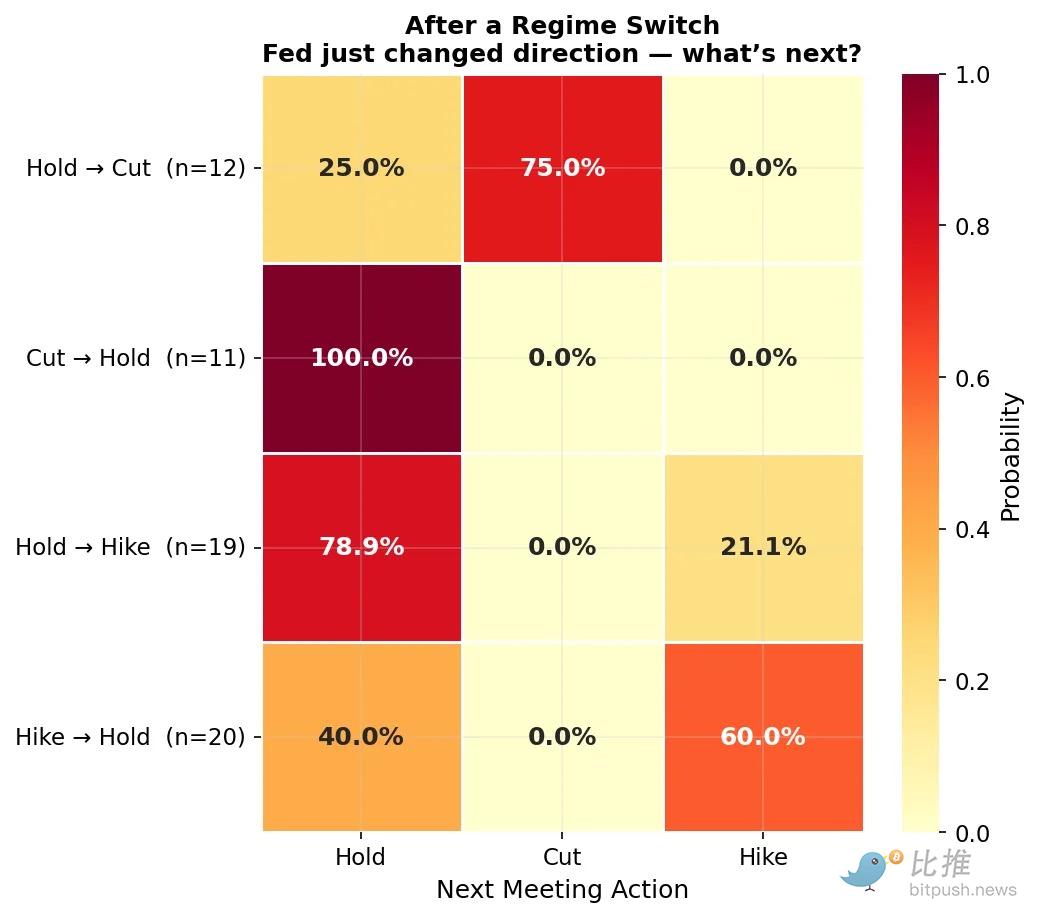
（图4：制度切换后，不同方向的变化差异巨大）
这是对交易者最有趣的部分。并非所有的方向改变都是平等的：
-
维持 -> 降息 -> 降息： 概率为 75%。一旦美联储打破维持状态开始首降，“闸门”就打开了，后续跟进概率极高。
-
降息 -> 维持 -> 维持： 概率为 100%。在近期历史中，美联储在暂停降息后从未立即恢复降息。一次暂停就意味着彻底停下！
-
维持 -> 加息 -> 维持： 概率为 79%。维持期后的第一次加息往往是试探性的，他们会停下来观察影响。
-
加息 -> 维持 -> 加息/维持： 分别为 60% 和 40%。与降息不同，加息途中的暂停具有真实的不确定性。
这里的不对称性是核心见解。“维持 -> 降息 -> 降息”的组合价值远高于简单乘法算出的价格。而“降息 -> 维持 -> 降息”这种组合在历史上价值几乎为零。同样的事件结果，仅仅顺序不同，其真实价值就天差地别。 独立乘法模型无法捕捉到这一点。
整体定价意味着什么？
这是整体情况。我们不应该使用盲目的平均概率，而应该使用历史观察到的条件概率。
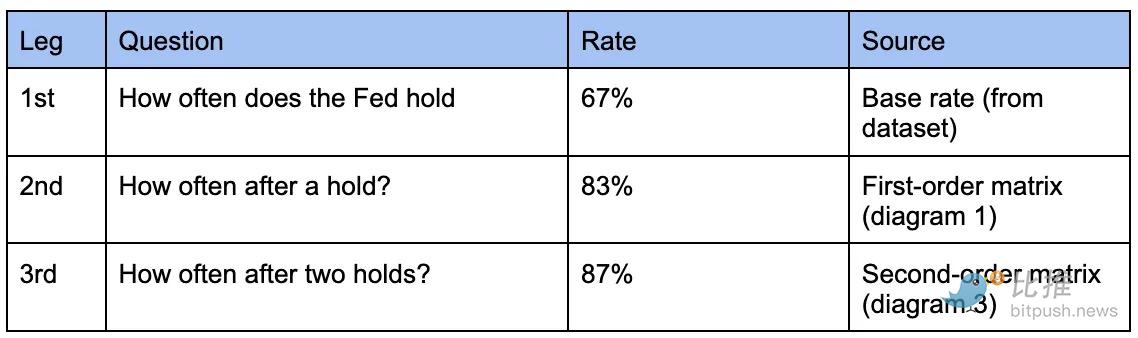
以“连续三次维持利率（Hold-Hold-Hold）”为例：
-
初始模型： 使用总概率（维持概率 67%），计算为 67% × 67% × 67% = 30.1%。
-
修正模型： 使用条件概率，计算为 67%（第一次）× 83%（第二次|第一次）× 87%（第三次|前两次）= 48.4%。
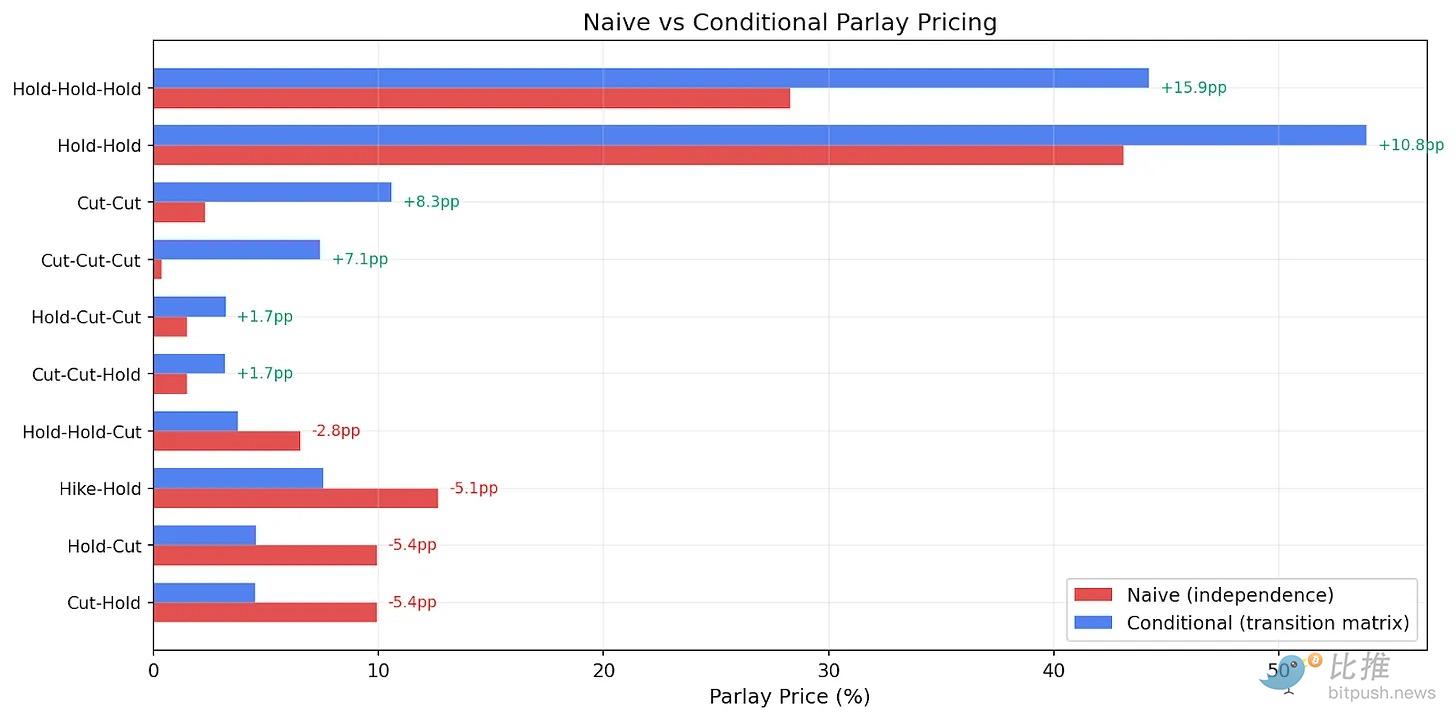
（图5：同向操作的组合被系统性低估，而涉及方向切换的组合则被高估）
实时市场检测
以 Polymarket 的数据为例：
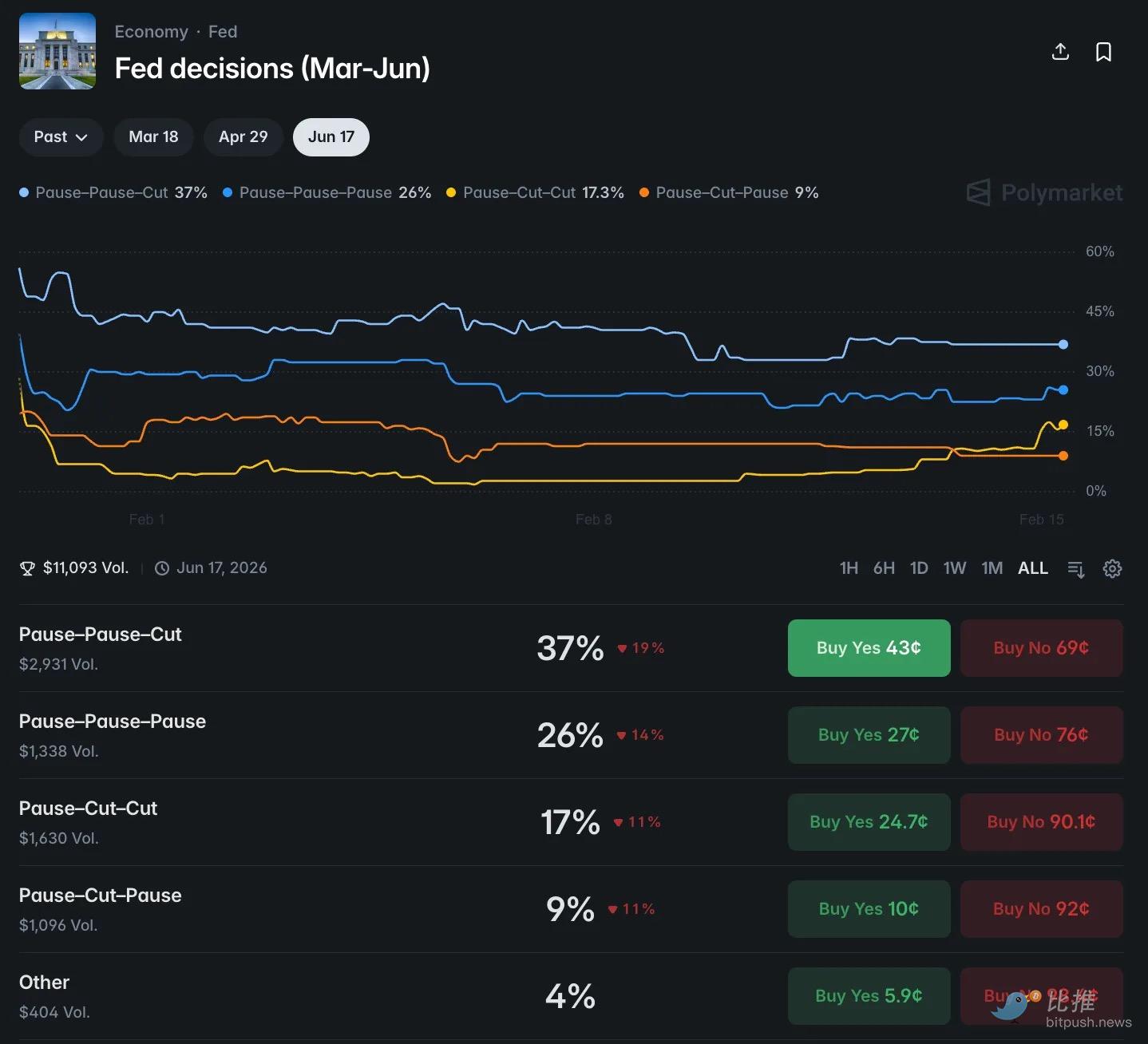
（图6：Polymarket 赔率分布与实际概率的对比）
组合一：维持 – 维持 – 维持（被严重低估）
-
初始模型定价： 93%（3月）× 75%（4月）× 38%（6月）≈ 26%
-
条件概率定价： 87% × 87% × 87% ≈ 65.8%
-
结论： 市场存在高达 39 个百分点 的严重低估。
组合二：维持 – 维持 – 降息（被严重高估）
-
初始模型定价： 93% × 75% × 49% = 34.2%
-
条件概率定价： 87% × 87% × 8.5% = 6.4%
-
结论： 市场定价约为 34%，而实际概率仅为 6.4%。市场价格高估了 5 倍以上。
这能赚钱吗？
我进行了一个简单的回测。自 1994 年以来的每一对和每一组三连美联储会议，如果修正后的价格高于市场价格（意味着被低估），就下注 100 美元。
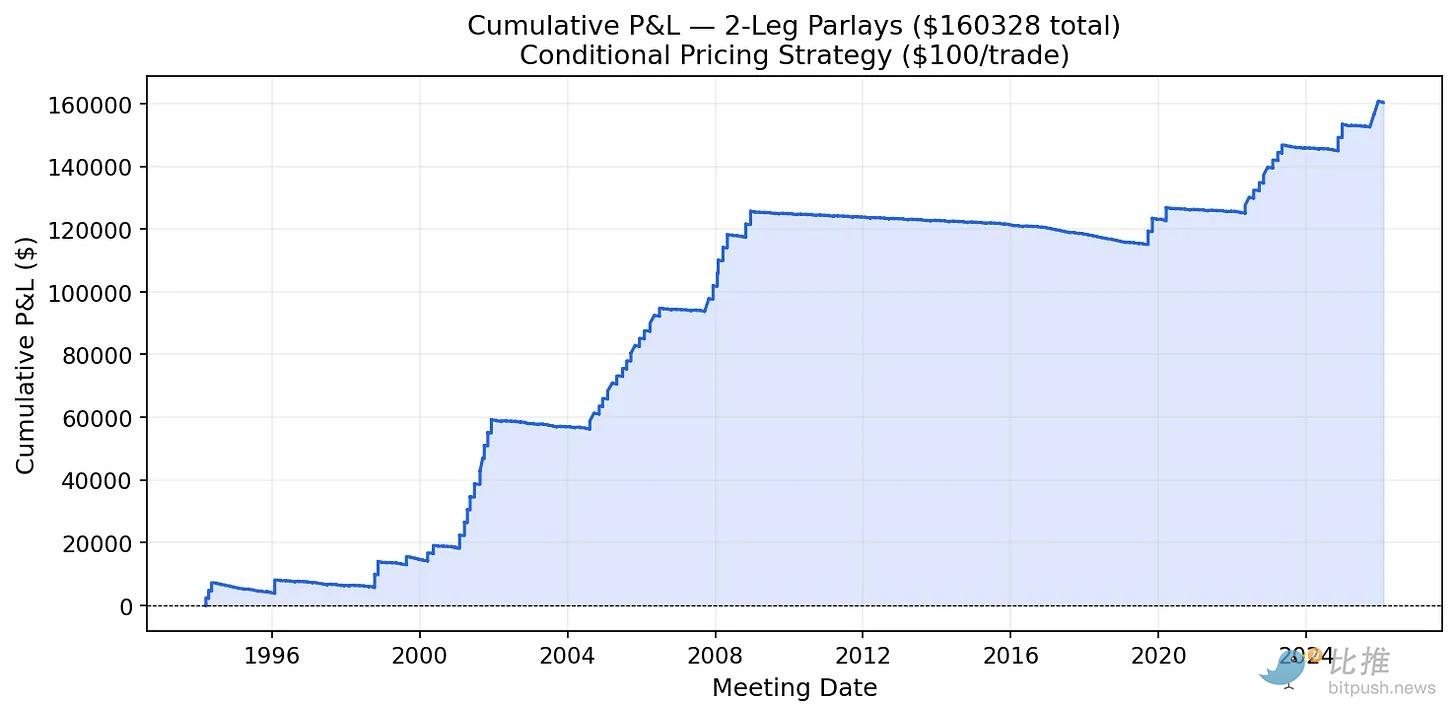
（图7：两连串关累积盈亏示例）
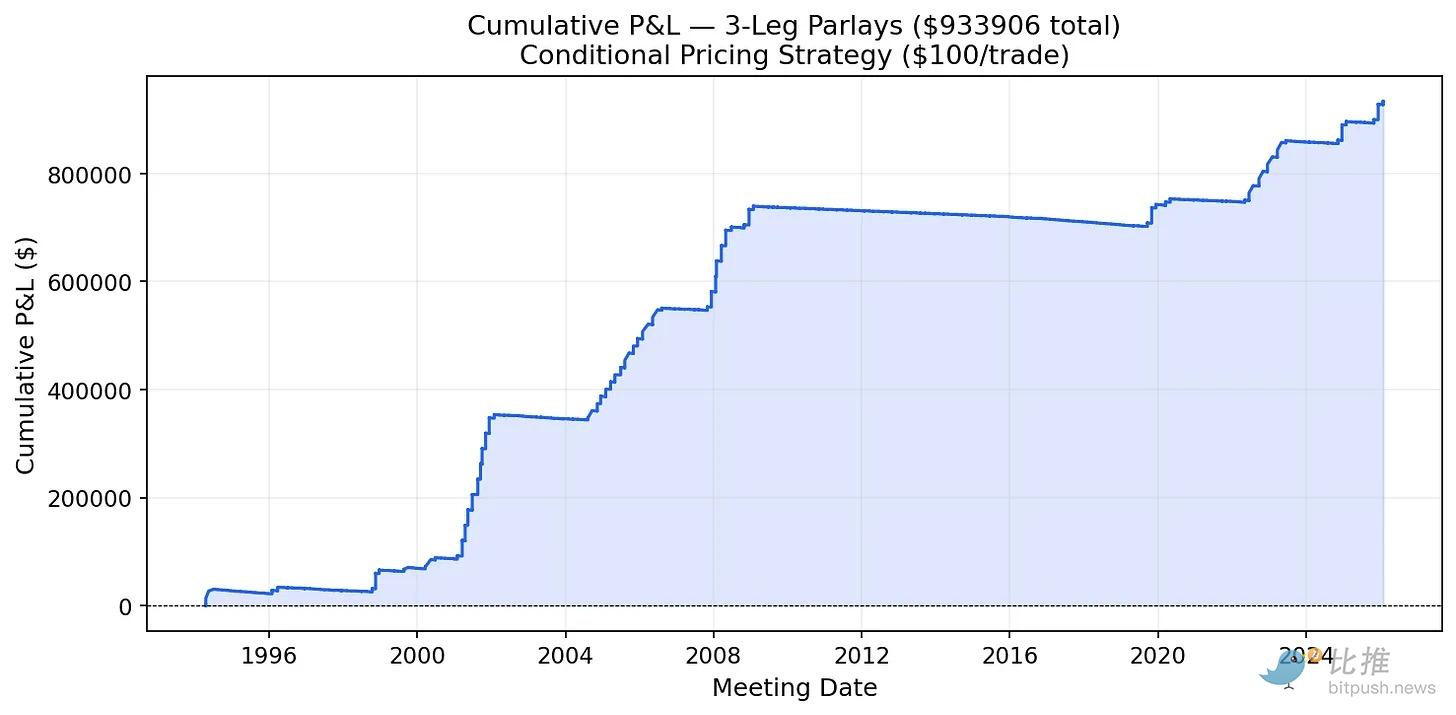
（图8：三连串关累积盈亏示例）
自 1994 年以来，对每个低估组合下注 100 美元，在两连串关上可产生 16.9 万美元收益，在三连串关上收益超过 100 万美元。收益曲线的大幅跳升对应美联储在 2001、2008、2020 以及 2024-2025 年的宽松周期。在这些周期中，连续的相同动作反复发生，而初始模型却一直在低估这种连贯性。
曲线的“阶梯状”告诉我们，钱是在美联储持续行动的周期中赚到的。不过，局限性在于，20 世纪 90 年代到 2000 年代可能并没有完善的预测市场来执行这些交易。
除了美联储，还能应用在哪里？
美联储案例很典型，因为数据充足且相关性强。但同样的框架适用于任何有关联的事件：
-
总统候选人初选： 如果一个候选人在一个州获胜，他在人口结构相似的州的胜算会改变。
-
加密货币与宏观/成长股： 比特币的走势与宏观风险偏好相关。赌“比特币高于 X 且纳斯达克高于 Y”的价值，高于两者独立概率的乘积，因为它们共享共同的驱动因素。
在任何情况下，方法都是一样的：查看历史数据，衡量事件之间的真实联系，使用更好的数据代替盲目的平均值，并与市场价格进行对比。
结论
预测市场仍处于初级阶段。大多数散户参与者在为“串关”定价时，仍在沿用那种“简单相乘、听天由命”的初级方式。
这个框架需要结合具体情境的知识，但归根结底只有一个问题：第一个事件的结果能否告诉你关于下一个事件的一些信息？ 如果能，那么天真的串关价格就是错的，而历史数据会告诉你具体错在多少。
美联储的案例研究表明，这种优势是真实存在且可衡量的。但这个原则是普遍适用的。在任何将相关事件作为独立事件定价的地方，都可能存在着未被发现的机会。
唯一的问题是，你是否能看见它，并采取行动。
Twitter：https://twitter.com/BitpushNewsCN
比推 TG 交流群：https://t.me/BitPushCommunity
比推 TG 订阅： https://t.me/bitpush
(来源:比推)
说明: 比推所有文章只代表作者观点，不构成投资建议
关联资讯:
分析：BTC 或在加息周期中上涨，货币宽松政策可能不再是牛市催化剂
分析师：比特币每日净买入量仍大于开采量，但科技股下跌或将导致比特币持续承压
深度研报：Fintech 靠抽成躺赢，DeFi 流水万亿却只赚零头
最频繁宣称四年周期已死的 Bitwise CIO，现在承认加密因四年周期陷入熊市
