35岁北大校友突破125年数学难题!网友:华人数学奇迹年 | 量子位
35岁北大校友突破125年数学难题!网友:华人数学奇迹年
从牛顿定律数学推导流体力学方程
时隔125年,著名的希尔伯特第六问题,终于被华人解决了!

这项研究共有三位作者,包括:
- 邓煜,芝加哥大学教授,北大(07级)/MIT校友
- 马骁,密歇根大学助理教授,本科毕业于中科大少年班
- Zaher Hani:密歇根大学教授,师从陶哲轩
希尔伯特第六问题,是David Hilbert在1900年提出的23个数学问题之一,要求通过公理化方法推导物理定律。
具体而言,就需要作者们从微观的牛顿力学出发,通过玻尔兹曼(Boltzmann)动力学理论,推导出流体力学中的基本方程。
而他们的这一成果不仅具有理论上的重要意义,也为流体力学的研究提供了新的数学工具。
可以说是对数学界和物理界都产生了重要的影响。
小红书网友“数学五人组”(五位在德国、法国读纯数学博士生们的账号)给出了这样的评价:
不仅如此,网友们结合之前北大校友王虹(91年生,16岁考入北大,07级)破解了挂谷猜想,直呼“北大数学系不愧中华第一系”、“07级真的太牛了”。
那么希尔伯特第六问题,到底是如何解的?我们一起来看下论文~
从牛顿经典力学到流体运动定律
1900年,在巴黎举行的第二届国际数学家大会上上,德国数学家大卫·希尔伯特提出了23道难题,被称为“希尔伯特的23个问题”。
我们比较熟悉黎曼猜想、哥德巴赫猜想,以及孪生素数猜想,共同作为的第八个问题被列入了其中,而这次三人组合解决的是其中的第六个问题,也就是“公理化物理”。
略显与众不同的是,“公理化物理”不是一个具体的数学表达式,更像一种数学思想,它的核心内容是这样的:
具体来说,希尔伯特希望类比欧几里得几何的公理化过程,给物理学也构建一个基于数学逻辑的严格体系。
希尔伯特在后续讨论中,将问题拆分为两个关键目标——
- 一是概率论的公理化基础,这一部分已经在20世纪上半叶被解决;
- 其二,就是从原子论到连续介质运动定律的数学极限过程。
再说简单些,就是从牛顿运动定律(微观)出发,用数学方法推导出流体的运动方程(宏观),而其中起到过渡作用的极限方法,就是玻尔兹曼方程(介观)。

但牛顿运动定律是可逆的,玻尔兹曼方程却是不可逆的,如何实现两者之间的转换,成了破解希尔伯特第六问题的关键。
包括希尔伯特本人在内,科学家们一直在尝试通过将玻尔兹曼方程展开等方式来完成这一过程。
直到1975年,美国数学家Oscar Lanford证明了兰福德定理,表明宏观不可逆性和微观可逆性之间的概念差距在原则上是可以克服的,为希尔伯特第六问题的解决奠定了基础。
直到去年,邓煜等三人联手,用一篇164页的论文,从稀薄气体硬球系统严格推导了玻尔兹曼动力学方程,使得希尔伯特第六问题的解决之路又向前迈进了一大步。

在这篇论文当中,作者采用累积量解析方法,通过引入累积量假设来追踪粒子碰撞的完整历史。
其核心步骤是将硬球动力学的演化表示为一系列费曼图结构,称为碰撞历史分子,并证明这些累积量在L1空间中的小性(smallness),即其对玻尔兹曼极限的渐近收敛性。
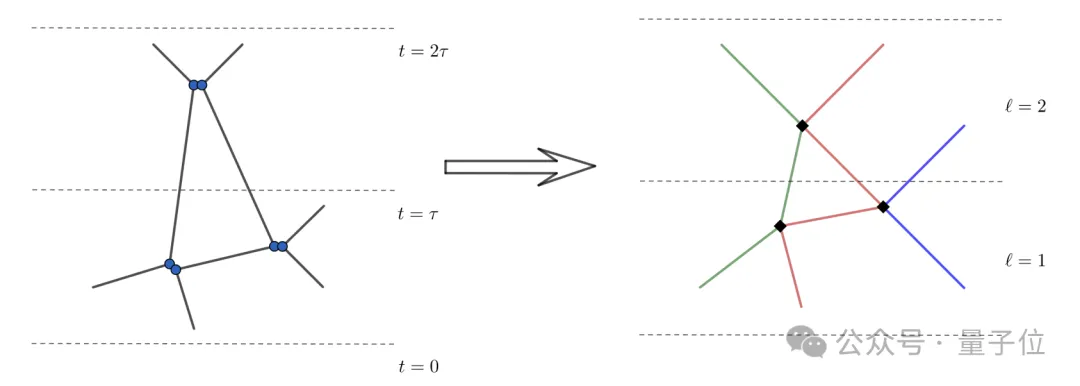
关键部分是通过一个复杂的“切割算法”来控制这些分子的组合性质,确保其中的复碰撞数量受限,以消除导致发散的因素。
最终,研究者证明,在整个玻尔兹曼方程解的存在时间范围内,累积量的贡献是可控的,从而严格推导出玻尔兹曼方程的长期有效性。
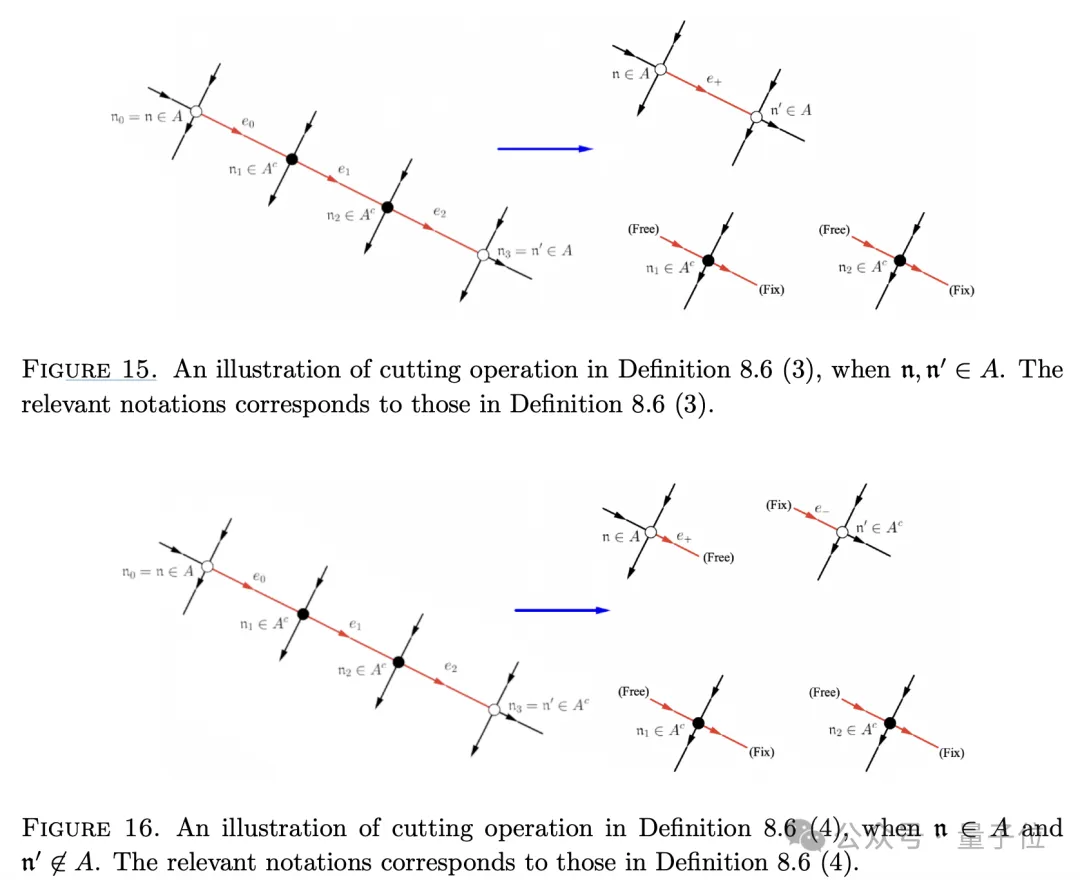
在此基础之上,刚刚发表的新论文终于给给狭义希尔伯特第六问题画上了圆满的句号,并在此基础上推导出了可压缩流体的欧拉方程以及不可压缩条件下的Navier-Stokes-Fourier方程。

作为此前工作的拓展,作者在2维和3维周期环面上推导了玻尔兹曼方程。
考虑一个由N个直径为ε的粒子组成的硬球系统,假设粒子之间发生弹性碰撞,运动满足牛顿定律。取Boltzmann-Grad极限,即N趋于无穷、ε趋于0,而Nεd-1保持为常数α。
在这个尺度下,作者证明了粒子系统的s粒子关联函数收敛到玻尔兹曼方程的解,其中s远小于总粒子数N,这一步将微观的粒子系统与介观的动理论方程玻尔兹曼方程联系了起来。
接下来考虑从玻尔兹曼方程到宏观流体力学方程的极限过程。在碰撞率α趋于无穷时,物理上对应于稀薄气体的平均自由程趋于0,宏观上体现为流体的连续介质极限。
数学上已有结果表明,在一定条件下,玻尔兹曼方程的局部Maxwellian形式的解会收敛到流体力学方程的解。
最后,将上述从粒子系统到玻尔兹曼方程、再从玻尔兹曼方程到流体力学方程的极限过程结合起来,取迭代极限,先固定α让N趋于无穷、ε趋于0,再让α趋于无穷,论文证明了粒子系统的物理量的极限满足宏观流体力学方程。
这就完成了Hilbert第六问题的方案,即从微观粒子系统的牛顿定律出发,通过玻尔兹曼动力学理论,严格推导出了宏观流体力学偏微分方程。
作者简介
如开头介绍,这项研究院由芝加哥大学教授邓煜、密歇根大学的Zaher Hani教授和马骁助理教授共同完成。
邓煜毕业于深圳高级中学,之后(来源:量子位)

